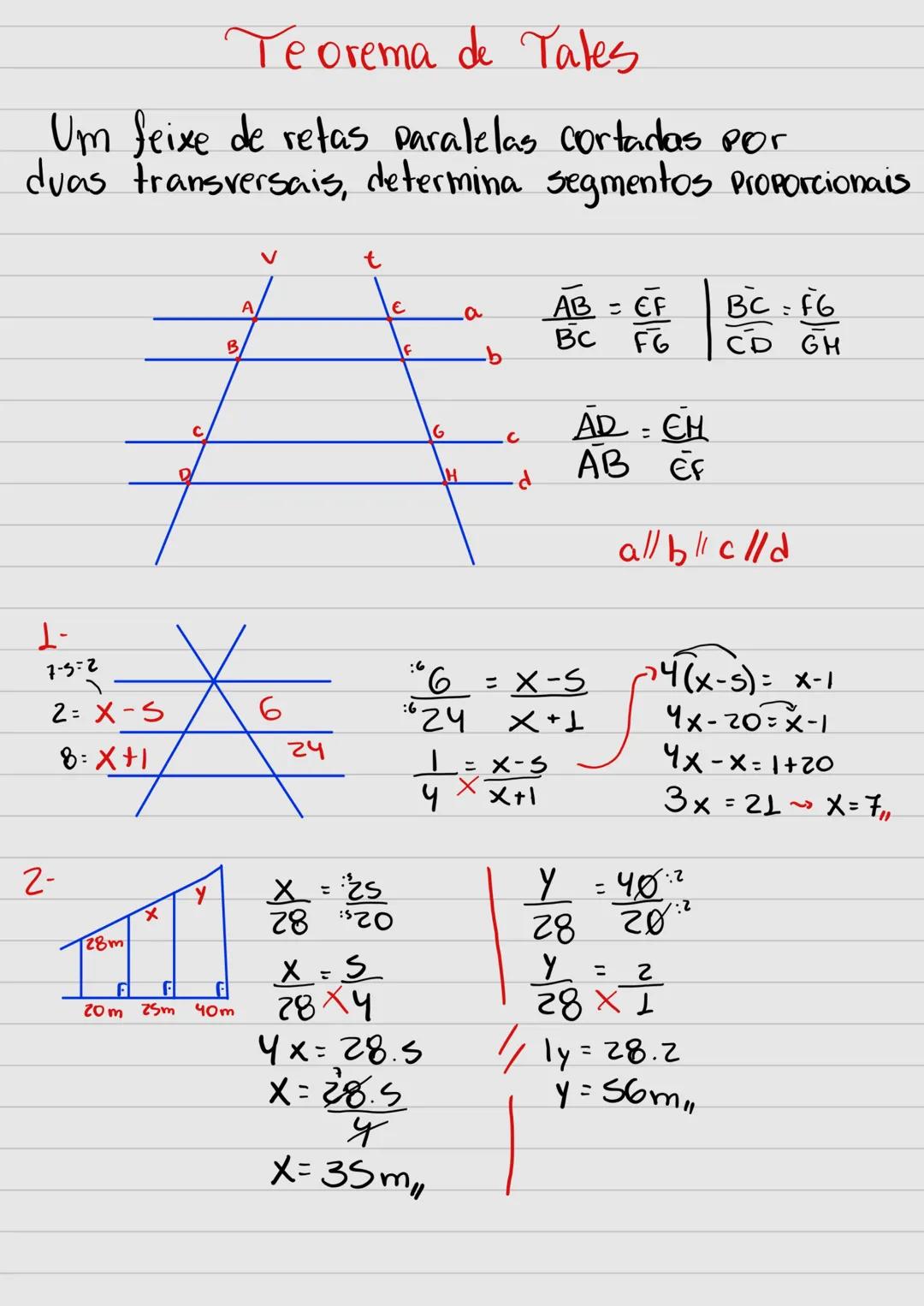
Teorema de Tales

Quando um feixe de retas paralelas é cortado por duas retas transversais, os segmentos determinados em uma transversal são proporcionais aos segmentos correspondentes na outra transversal. Em outras palavras, se temos retas paralelas cortadas por transversais, podemos estabelecer que: AB/BC = EF/FG e BC/CD = FG/GH.

Esta proporção é a base do Teorema de Tales e nos permite resolver diversos problemas geométricos. Por exemplo, quando conhecemos três segmentos em uma configuração de Tales, podemos calcular o quarto usando uma simples regra de três. Isso é extremamente útil para determinar distâncias inacessíveis.

A aplicação do teorema aparece em várias situações práticas, como no cálculo de altura de objetos usando sombras, na resolução de problemas de semelhança de triângulos e em construções geométricas. Os exemplos mostram como podemos usar equações como 8:X = 2:$X-5$ para encontrar valores desconhecidos.

Dica importante: Sempre mantenha a ordem dos segmentos ao montar as proporções! Se você começar com AB/BC na primeira transversal, deve usar EF/FG (segmentos correspondentes) na segunda transversal.

O teorema também pode ser aplicado em situações mais complexas, envolvendo múltiplas retas paralelas e proporções encadeadas. Dominando este conceito, você terá uma ferramenta poderosa para resolver problemas de geometria no vestibular e no ENEM.