Tipos de Funções Lineares

A função identidade $f(x) = x$ é o caso mais simples, onde a imagem de qualquer valor é ele mesmo. Seu gráfico é a bissetriz dos quadrantes 1 e 3 no plano cartesiano.

A função linear tem a forma $f(x) = ax$, com $a ∈ ℝ$. Seu gráfico é sempre uma reta não vertical passando pela origem. Esta é um caso particular da função polinomial do 1º grau.

Já a função polinomial do 1º grau é representada por $f(x) = ax + b$, com $a ≠ 0$ e $b ∈ ℝ$. Exemplos: $f(x) = 3x + 5$ ou $y = 2x - 1$. Tanto o domínio quanto a imagem destas funções é o conjunto dos números reais (ℝ).

💡 Dica prática: Para identificar rapidamente uma função do 1º grau, basta verificar se a variável x aparece com expoente 1 e se não há potências maiores de x na expressão.

O coeficiente angular (a) determina a inclinação da reta. Matematicamente, é a tangente do ângulo formado entre a reta e o eixo x, calculado por $a = \frac{\Delta y}{\Delta x}$ (a variação de y dividida pela variação de x).

Análise Gráfica da Função

O coeficiente linear (b) indica onde a reta cruza o eixo y. Quando substituímos $x = 0$ na função $f(x) = ax + b$, encontramos $f(0) = b$, o que nos dá o ponto $(0,b)$.

A raiz ou zero da função é o valor de x que torna a função igual a zero. Esse valor representa o ponto onde o gráfico cruza o eixo x. Para encontrá-lo, basta resolver a equação $ax + b = 0$, obtendo $x = -\frac{b}{a}$. Por exemplo, na função $f(x) = 2x - 6$, o zero é $x = 3$.

Para desenhar o gráfico de uma função do 1º grau, precisamos de apenas dois pontos, já que o resultado é sempre uma reta. Você pode encontrar esses pontos usando dois métodos principais:

1. Método da tabela de valores: Escolha dois valores para x, substitua na função e calcule os valores correspondentes de y. Por exemplo, para $f(x) = 2x - 2$, podemos usar $x = 2$ e $x = 4$, encontrando os pontos $(2, 2)$ e $(4, 6)$.

⚠️ Atenção: Escolha valores para x que resultem em cálculos simples para evitar erros. O zero da função e a interseção com o eixo y são normalmente boas escolhas!

Construindo e Identificando Funções

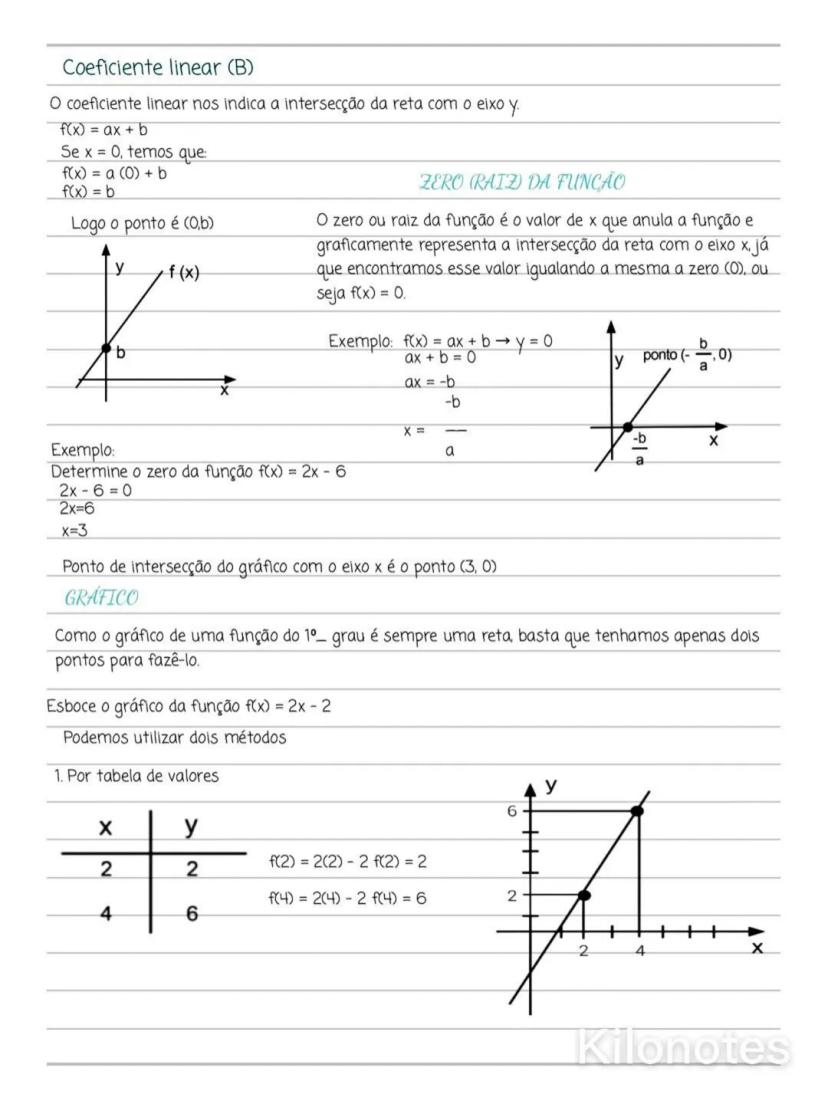
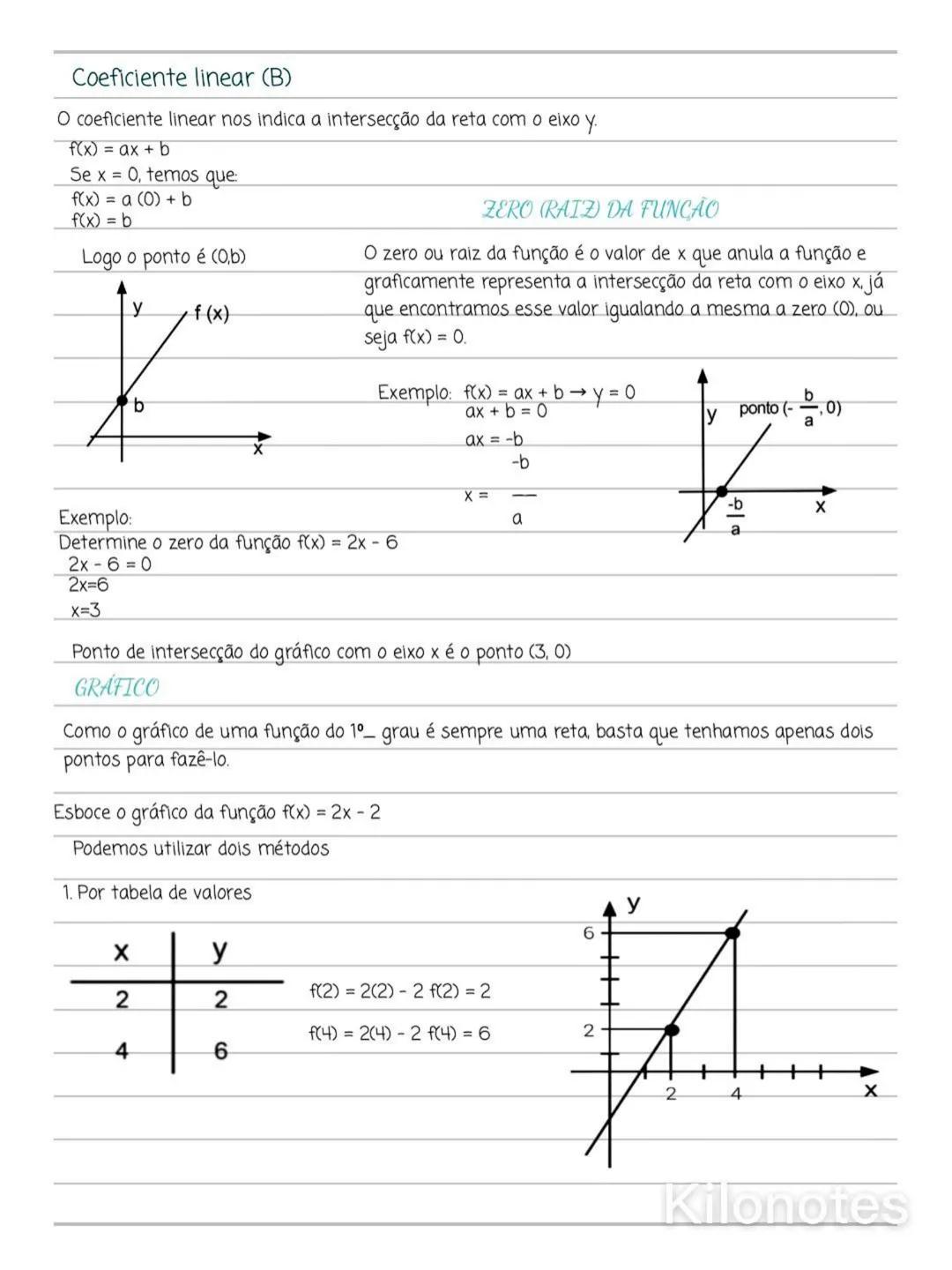
O segundo método para desenhar o gráfico usa o coeficiente linear e o zero da função. Para $y = 2x - 2$, identificamos que a reta passa pelos pontos $(0, -2)$ (coeficiente linear) e $(1, 0)$ (zero da função).

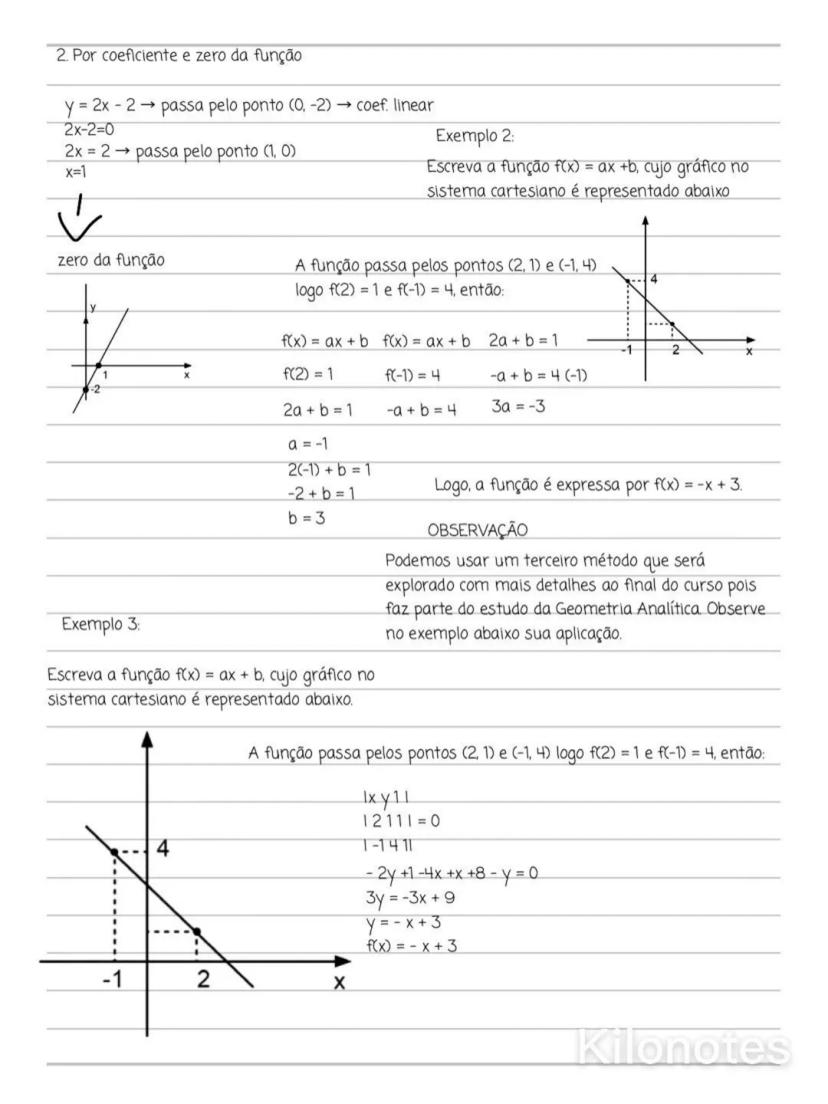
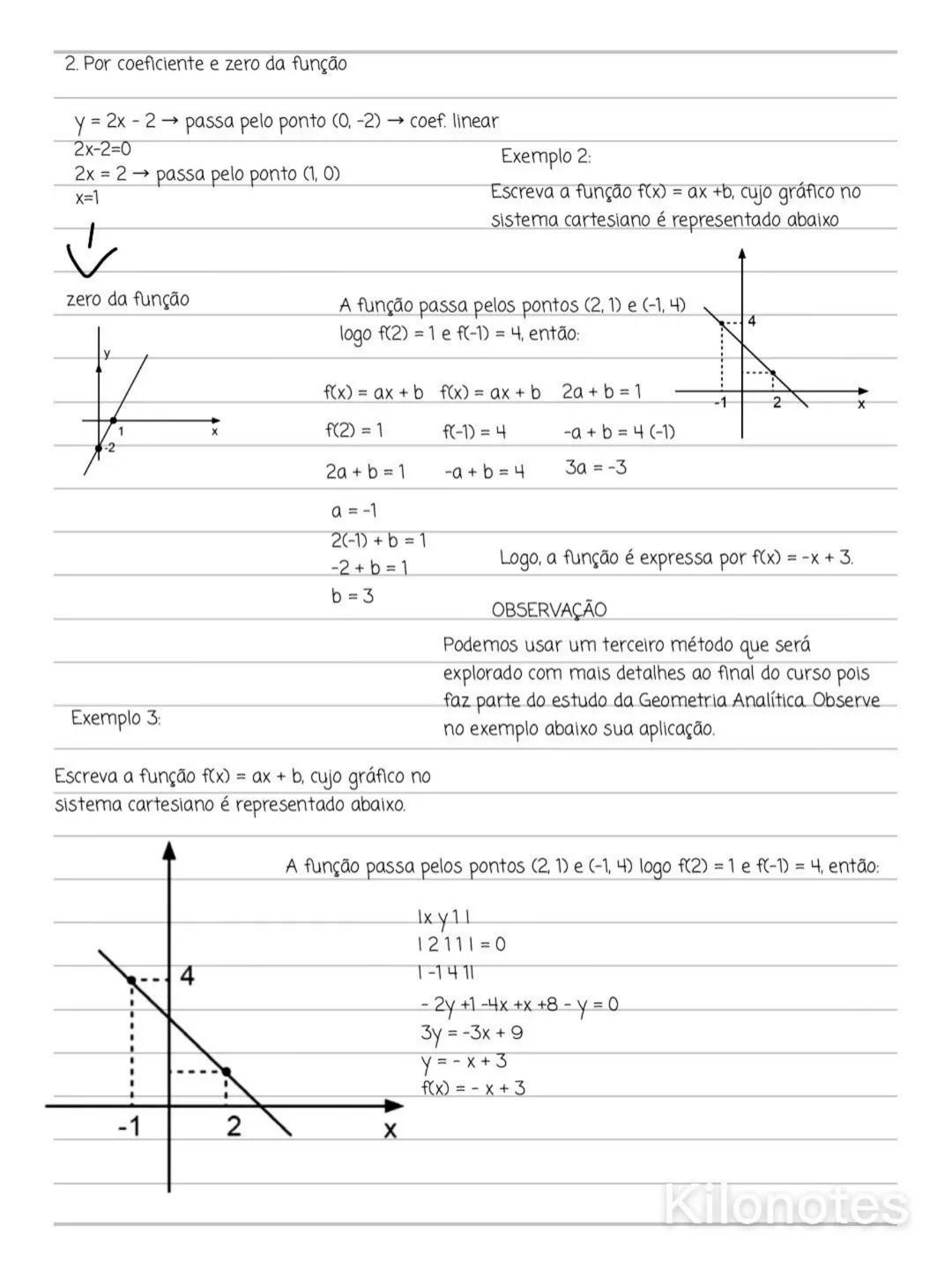
Também podemos encontrar a função a partir de dois pontos do seu gráfico. Quando sabemos que uma reta passa por dois pontos, podemos determinar os coeficientes a e b resolvendo um sistema de equações.

Por exemplo, se uma reta passa pelos pontos $(2, 1)$ e $(-1, 4)$, substituímos na forma $f(x) = ax + b$:

• Para $(2, 1)$: $1 = 2a + b$
• Para $(-1, 4)$: $4 = -a + b$

Resolvendo o sistema, encontramos $a = -1$ e $b = 3$, resultando em $f(x) = -x + 3$.

Um terceiro método para encontrar a equação da reta vem da Geometria Analítica, que permite determinar a função a partir de características geométricas da reta.

💡 Simplificando: A equação de uma reta sempre segue o padrão $y = ax + b$. Uma vez que você conheça dois pontos, pode encontrar os valores de a e b com um sistema simples de duas equações.

Dominar estas técnicas permite que você resolva problemas práticos envolvendo relações lineares em várias áreas, desde física até economia!