Matemática: Conceitos e Aplicações

A Matemática vai muito além de simples cálculos com números. É uma linguagem poderosa que nos permite compreender padrões e relações no mundo ao nosso redor.

Você já percebeu como a Matemática está presente em quase tudo que fazemos? Desde calcular o troco em uma compra até analisar gráficos de crescimento populacional, os conceitos matemáticos são ferramentas essenciais.

Neste material, vamos explorar os fundamentos matemáticos que servirão como base para seus estudos futuros, apresentando de forma clara os principais conceitos e suas aplicações práticas.

Dica: Não se preocupe se alguns conceitos parecerem complexos no início. A matemática é como um quebra-cabeça onde cada peça se encaixa perfeitamente nas outras quando você entende a lógica por trás.

Introdução ao Material

Este material foi desenvolvido para ajudar estudantes a compreender os fundamentos da matemática de forma clara e objetiva.

Os conteúdos foram organizados de maneira progressiva, começando pelos conceitos mais básicos até chegar aos mais complexos. Isso permite que você construa seu conhecimento passo a passo.

A matemática pode parecer desafiadora à primeira vista, mas com prática e dedicação, você perceberá que é uma disciplina lógica e fascinante.

Se você encontrar dificuldades em algum tópico, não desista! Reveja os conceitos anteriores, faça os exercícios propostos e busque exemplos adicionais que possam ajudar na compreensão.

Lembre-se que a matemática é uma habilidade que se desenvolve com prática. Quanto mais você exercitar, mais fácil ficará!

Conjuntos Numéricos

Os conjuntos numéricos são a base de toda a matemática. Eles organizam os números de acordo com suas propriedades e características.

O conjunto dos números naturais (ℕ) inclui todos os números inteiros positivos: ℕ = {1, 2, 3, ...}

Já o conjunto dos números inteiros (ℤ) adiciona o zero e os negativos: ℤ = {..., -3, -2, -1, 0, 1, 2, 3, ...}

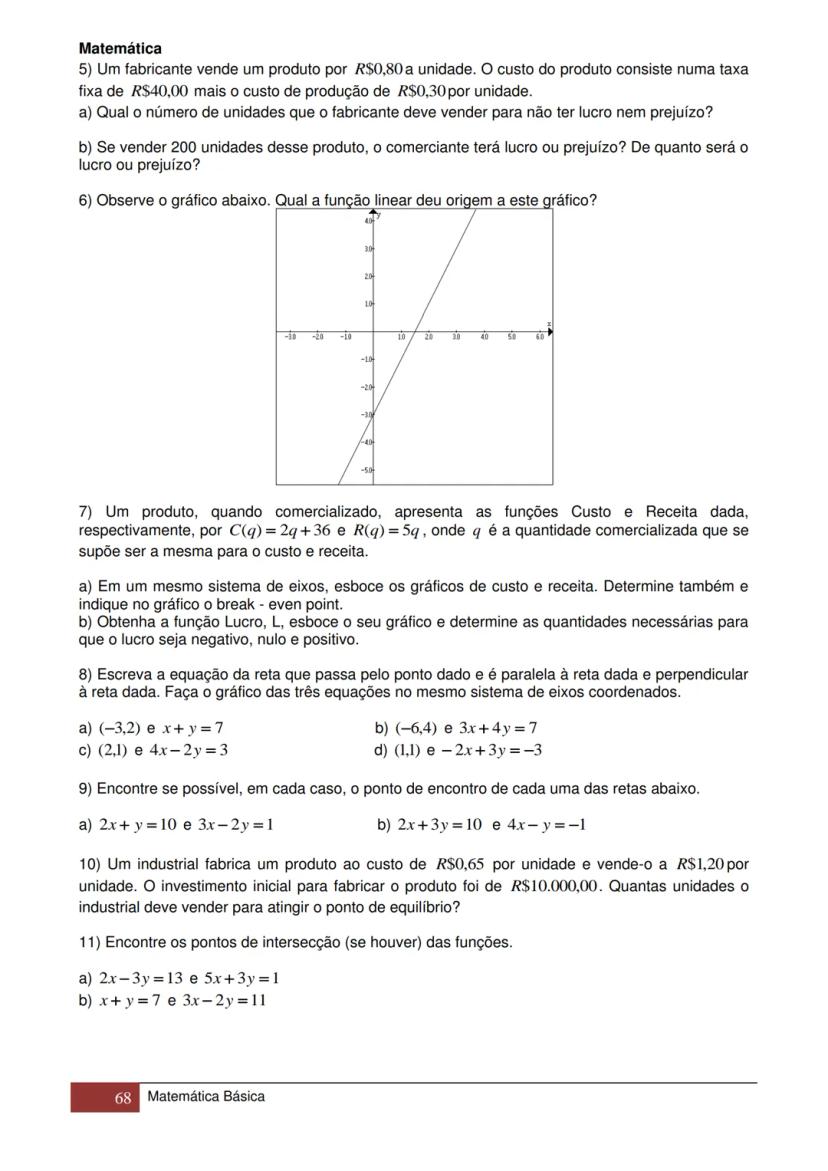
Os números racionais (ℚ) são aqueles que podem ser expressos como fração de dois inteiros: ℚ = {p/q | p ∈ ℤ, q ∈ ℤ, q ≠ 0}

Números racionais podem ser representados como decimais finitos (7/4 = 1,75) ou como dízimas periódicas (1/3 = 0,3333...).

Existem também os números irracionais (𝕀), que não podem ser expressos como fração e possuem representação decimal infinita não periódica, como π = 3,141592... e √2 = 1,4142...

Curiosidade: Sabia que existem infinitamente mais números irracionais do que racionais, apesar de os racionais também serem infinitos? Isso é um exemplo fascinante do conceito de "tamanho" de infinitos!

Operações entre Conjuntos

As operações entre conjuntos permitem manipular grupos de elementos de forma organizada e precisa.

A união de conjuntos A e B (A ∪ B) contém todos os elementos que pertencem a A ou a B. Por exemplo, se A = {1, 2, 3, 5} e B = {3, 4, 5, 7}, então A ∪ B = {1, 2, 3, 4, 5, 7}.

A interseção de conjuntos A e B (A ∩ B) contém os elementos comuns a ambos. Usando o exemplo anterior, A ∩ B = {3, 5}.

Quando a interseção entre conjuntos é vazia $A ∩ B = ∅$, dizemos que eles são conjuntos disjuntos.

A diferença entre conjuntos A e B $A - B$ contém os elementos de A que não pertencem a B. Assim, A - B = {1, 2}.

Os intervalos são subconjuntos importantes dos números reais:

• Intervalo aberto: (a,b) = {x ∈ ℝ | a < x < b}
• Intervalo fechado: $a,b$ = {x ∈ ℝ | a ≤ x ≤ b}
• Intervalo semi-aberto: $a,b) ou (a,b$

Atenção! Ao resolver problemas com conjuntos, sempre verifique se os elementos satisfazem as condições necessárias para pertencer ao conjunto resultante da operação.

Expressões Numéricas

As expressões numéricas são combinações de números e operações que devem ser resolvidas seguindo uma ordem específica.

Para resolver expressões numéricas, siga esta ordem:

1. Resolva primeiro o que está dentro dos parênteses ()
2. Em seguida, colchetes $$ e chaves {}
3. Realize potências e raízes
4. Faça multiplicações e divisões, na ordem em que aparecem
5. Por último, realize adições e subtrações

Por exemplo: 2+$2-(3+2)-1$ = 2+$2-5-1$ = 2+$2-6$ = 2+$-4$ = -2

A decomposição de um número em fatores primos é útil para encontrar o mínimo múltiplo comum (MMC) e o máximo divisor comum (MDC).

Para encontrar o MMC entre dois ou mais números:

• Decomponha cada número em fatores primos
• Multiplique os fatores primos com os maiores expoentes

Para encontrar o MDC:

• Decomponha cada número em fatores primos
• Multiplique os fatores primos comuns com os menores expoentes

Dica prática: Para decompor um número em fatores primos, divida-o sucessivamente pelos menores números primos (2, 3, 5, 7...) até obter 1 como resultado.

Frações e Operações

As frações representam partes de um todo e são expressas como a/b, onde a é o numerador e b é o denominador (b ≠ 0).

Uma fração é própria quando o numerador é menor que o denominador $como 3/5$. É imprópria quando o numerador é maior que o denominador $como 7/3 = 2⅓$.

Propriedades das frações:

P1: Multiplicação por um número Multiplicando ou dividindo ambos os termos pelo mesmo número (≠ 0), obtém-se uma fração equivalente: 1/2 = (1×2)/(2×2) = 2/4

P2: Soma de frações Para somar frações, é preciso igualar os denominadores usando o MMC: 1/3 + 1/6 = 2/6 + 1/6 = 3/6 = 1/2

P3: Multiplicação de frações Multiplique os numeradores entre si e os denominadores entre si: (1/2) × (3/4) = 3/8

P4: Divisão de frações Multiplique a primeira fração pelo inverso da segunda: (1/2) ÷ (3/4) = (1/2) × (4/3) = 4/6 = 2/3

Não se esqueça: Ao operar com frações, sempre verifique se é possível simplificar o resultado final!

Potências e Propriedades

A potência de um número a com expoente n é o produto de n fatores iguais a a, representada por aⁿ.

Propriedades importantes:

P1: Multiplicação de potências de mesma base Mantém-se a base e somam-se os expoentes: aᵐ × aⁿ = aᵐ⁺ⁿ Exemplo: 5² × 5⁷ = 5⁹

P2: Divisão de potências de mesma base Mantém-se a base e subtraem-se os expoentes: aᵐ ÷ aⁿ = aᵐ⁻ⁿ Exemplo: 3⁷ ÷ 3³ = 3⁴

P3: Potência de uma potência Mantém-se a base e multiplicam-se os expoentes: (aᵐ)ⁿ = aᵐⁿ Exemplo: (5³)² = 5⁶

P4: Potência de um produto (ab)ⁿ = aⁿbⁿ Exemplo: (5·3)² = 5²·3²

P5: Potência de um quociente $a/b$ⁿ = aⁿ/bⁿ, para b≠0 Exemplo: (5/3)² = 5²/3²

P6: Expoente negativo a⁻ⁿ = 1/aⁿ Exemplo: 5⁻² = 1/5² = 1/25

Observação: Qualquer número (exceto 0) elevado a 0 é igual a 1: a⁰ = 1

Radicais e Suas Propriedades

Um radical é uma expressão que representa a raiz de um número. A raiz n-ésima de a é escrita como ∛a.

Para simplificar radicais, podemos usar estas propriedades:

P1: Extrair do radical É possível retirar do radical um fator que seja potência do índice. √12 = √(2²·3) = 2√3

P2: Operações com radicais semelhantes Para radicais de mesmo índice e mesmo radicando, operamos os coeficientes: 3√2 + 5√2 - 10√2 = -2√2

P3: Multiplicação e divisão de radicais de mesmo índice Multiplique ou divida os radicandos mantendo o índice: √2 · √3 = √6 e √6 ÷ √2 = √3

P4: Potenciação de radicais (√a)ⁿ = √aⁿ Exemplo: (√2)³ = √2³ = √8

P5: Racionalização de denominadores Para eliminar radicais do denominador: 1/√2 = √2/2 (multiplicando numerador e denominador por √2)

P6: Expoente fracionário aᵐ/ⁿ = ⁿ√aᵐ Exemplo: 2²/³ = ³√2² = ³√4

Truque útil: Para racionalizar denominadores com radicais duplos como 1/(√5+√2), multiplique numerador e denominador pela expressão conjugada (√5-√2).

Operações Algébricas

As expressões algébricas são combinações de números e letras ligados por operações matemáticas. Elas nos permitem generalizar problemas e estabelecer relações.

1) Soma algébrica Apenas termos semelhantes (com mesma parte literal) podem ser somados ou subtraídos: 3x²y - 4xy² + 7xy² + 5x²y = 8x²y + 3xy²

2) Multiplicação Multiplique cada termo do primeiro fator por todos os termos do segundo: (3a²y)(2ay) = 6a³y²

3) Divisão Na divisão de polinômio por monômio, divide-se cada termo do polinômio pelo monômio: (42a³bx) ÷ (7ax²) = 6a²bx⁻¹

4) Produtos notáveis São fórmulas importantes que facilitam cálculos:

• Quadrado da soma: $a+b$² = a² + 2ab + b²
• Quadrado da diferença: $a-b$² = a² - 2ab + b²
• Produto da soma pela diferença: $a+b$$a-b$ = a² - b²

5) Fatoração Fatorar um polinômio é escrevê-lo como um produto. Um método é encontrar o fator comum: 5x²y + x²y³ + 2x² = x²$5y + y³ + 2$

Aplique na prática: A fatoração é muito útil para simplificar expressões e resolver equações. Sempre verifique se é possível fatorar antes de realizar outras operações mais complexas.

Números e Grandezas Proporcionais

As grandezas são valores que se relacionam entre si de forma que a variação de um causa variação no outro.

Grandezas diretamente proporcionais Quando a variação de uma implica variação da outra na mesma proporção e sentido. Exemplo: 1kg de carne custa R$20, então 2kg custará R$40.

Grandezas inversamente proporcionais Quando a variação de uma implica variação da outra na mesma proporção, mas em sentido contrário. Exemplo: Um carro a 100km/h percorre certa distância em 2 horas. A 200km/h percorrerá a mesma distância em 1 hora.

Razão é o quociente entre dois números: a razão de 9 para 12 é 9/12 = 3/4.

Proporção é a igualdade entre duas razões: a/b = c/d.

Propriedades das proporções:

• Em toda proporção, o produto dos meios é igual ao produto dos extremos: a/b = c/d → a·d = b·c
• Composição: a/b = c/d → $a+b$/a = $c+d$/c
• Decomposição: a/b = c/d → $a-b$/a = $c-d$/c

Dica prática: Nas questões de proporcionalidade, sempre identifique primeiro se as grandezas são diretamente ou inversamente proporcionais. Isso facilita muito a resolução!