Plano Cartesiano e Coordenadas

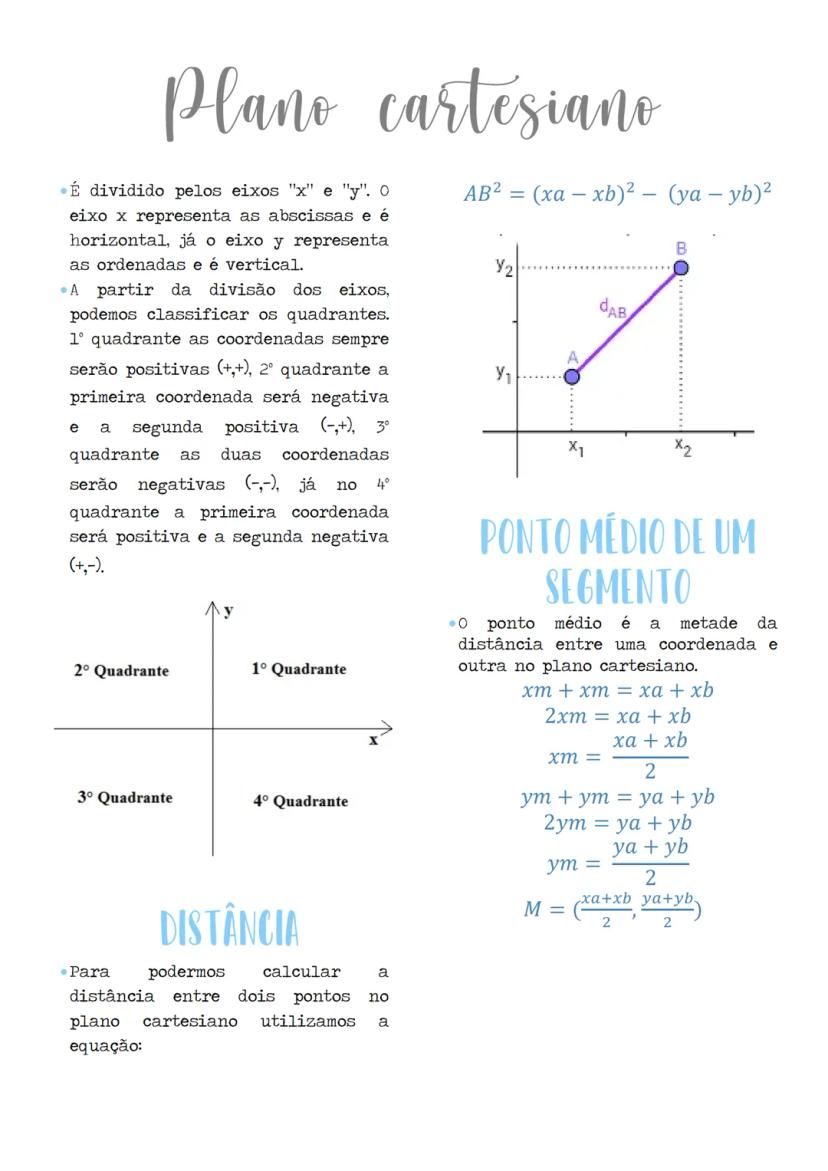
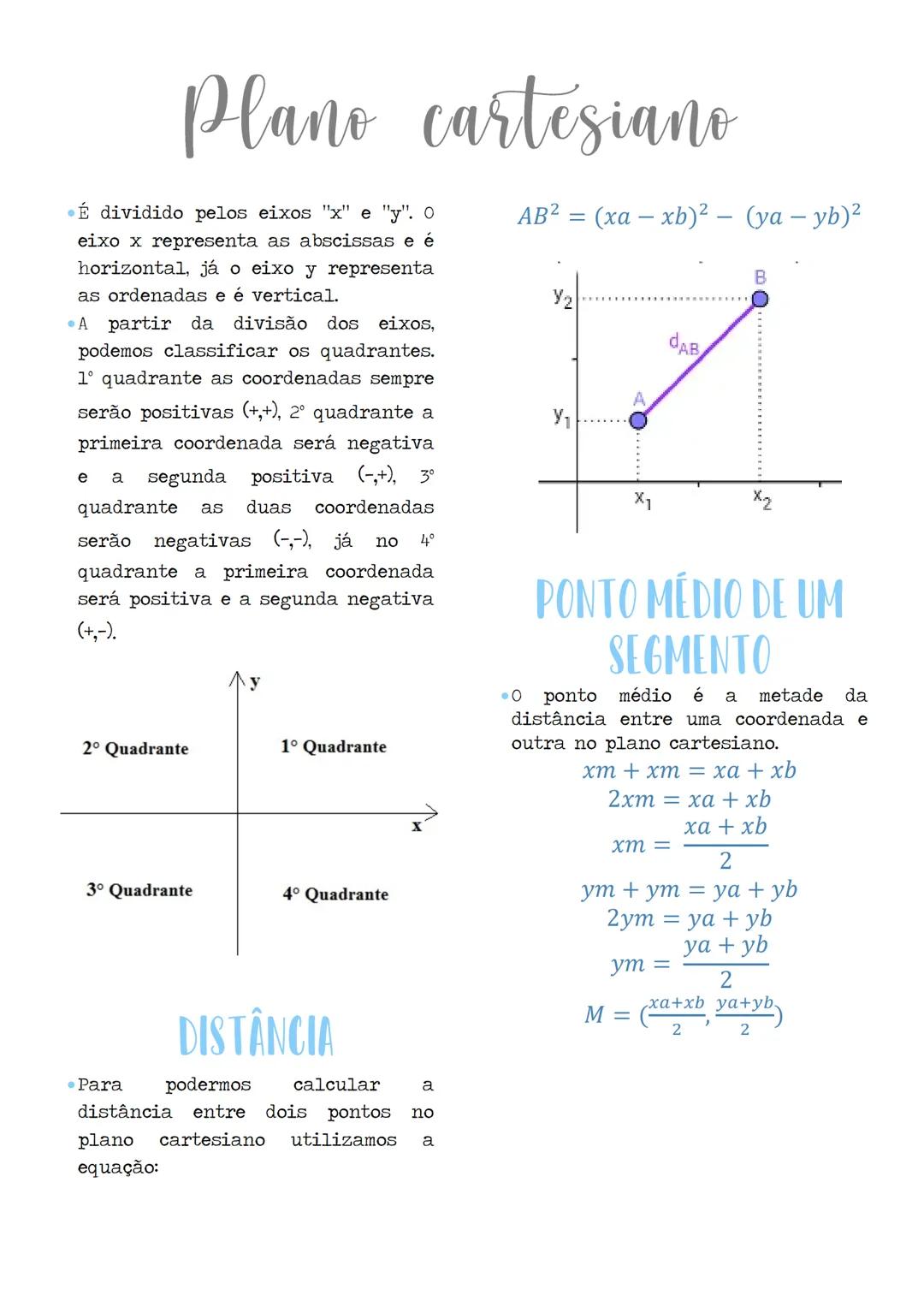
O plano cartesiano é dividido por dois eixos perpendiculares: o eixo x (horizontal, abscissas) e o eixo y (vertical, ordenadas). Essa divisão cria quatro quadrantes com características específicas.

No 1º quadrante, ambas coordenadas são positivas (+,+). No 2º quadrante, temos a primeira coordenada negativa e a segunda positiva (-,+). Já no 3º quadrante, ambas coordenadas são negativas (-,-). E no 4º quadrante, a primeira coordenada é positiva e a segunda negativa (+,-).

Para calcular a distância entre dois pontos no plano cartesiano, usamos a fórmula: AB² = $xa-xb$² - $ya-yb$². Essa equação permite determinar o comprimento exato entre quaisquer dois pontos.

💡 Dica prática: Para lembrar os sinais em cada quadrante, pense como se estivesse lendo um livro: comece no canto superior direito (+,+) e vá no sentido anti-horário.

O ponto médio de um segmento é encontrado calculando a média das coordenadas: M = $(xa+xb)/2, (ya+yb)/2$. Isso significa que o ponto médio está exatamente na metade do caminho entre os dois pontos originais.

Condição de Alinhamento e Equações da Reta

Existem duas maneiras de verificar se três ou mais pontos estão alinhados no plano cartesiano. A primeira utiliza a taxa de variação de uma função afim, calculada por a = Δy/Δx. Se essa taxa for constante entre todos os pares de pontos, eles estão alinhados.

A segunda forma envolve o uso de determinantes de matrizes. Para pontos alinhados, o determinante de uma matriz específica deve ser igual a zero. Em uma matriz 2x2, o determinante é calculado pelo produto da diagonal principal menos o produto da diagonal secundária.

Para matrizes 3x3, o cálculo é mais complexo. Copie as duas primeiras colunas ao lado da matriz original e multiplique as diagonais (mantendo sinais na direção principal e invertendo na direção oposta).

A equação geral da reta é representada por Ax + By + C = 0, onde A ou B são diferentes de zero. Essa forma algébrica permite analisar qualquer reta no plano cartesiano, independente de sua inclinação.

⚠️ Atenção! Quando dois pontos têm a mesma taxa de variação em relação a um terceiro ponto, os três estão garantidamente alinhados.

Interseção de Retas e Introdução às Matrizes

Quando duas retas são concorrentes, podemos encontrar o ponto de interseção organizando suas equações gerais e resolvendo o sistema resultante. Esse ponto é a única solução comum às duas equações.

Para resolver um sistema de equações lineares, podemos usar o método de substituição ou eliminação. Ao encontrar valores para x e y, obtemos as coordenadas exatas do ponto de interseção entre as retas.

Uma matriz é uma tabela organizada com m linhas e n colunas, contendo m·n elementos. Cada elemento é identificado pela notação aij, onde i indica a linha e j a coluna onde o elemento está localizado.

Existem vários tipos de matrizes especiais:

• Matriz linha: possui apenas uma linha (1×n)
• Matriz coluna: possui apenas uma coluna (m×1)
• Matriz nula: todos os elementos são iguais a zero
• Matriz quadrada: tem o mesmo número de linhas e colunas

💡 Dica útil: Nas matrizes quadradas, preste atenção às diagonais! A diagonal principal vai do canto superior esquerdo ao inferior direito, enquanto a diagonal secundária vai do canto superior direito ao inferior esquerdo.

Operações com Matrizes

Duas matrizes são iguais quando possuem o mesmo tipo (mesmas dimensões) e todos os seus elementos correspondentes são iguais. Por exemplo, se A e B têm os mesmos valores nas mesmas posições, então A = B.

A adição de matrizes só é possível entre matrizes de mesmo tipo. Somamos cada elemento correspondente: aij + bij = cij. Esta operação possui propriedades importantes como a comutatividade $A+B=B+A$, associatividade e existência de elemento neutro.

Para a subtração de matrizes, seguimos o mesmo princípio, subtraindo elementos correspondentes: aij - bij = cij. Na prática, subtrair B de A é o mesmo que adicionar o oposto de B a A.

A multiplicação por escalar ocorre quando multiplicamos todos os elementos de uma matriz por um número real. Por exemplo, 2·[5 0; 8 3] = [10 0; 16 6]. Esta operação distribui-se tanto em relação à soma de matrizes quanto à soma de escalares.

Já a multiplicação entre matrizes segue regras específicas. Para multiplicar A por B, multiplicamos cada elemento da linha de A pelo elemento correspondente da coluna de B e somamos os resultados. Para que seja possível, o número de colunas de A deve ser igual ao número de linhas de B.

⚠️ Importante! A ordem dos fatores altera o produto na multiplicação de matrizes. Em geral, A·B ≠ B·A, diferente da multiplicação de números reais.

Matriz Identidade e Matriz Inversa

A matriz identidade (I) é uma matriz quadrada especial onde todos os elementos da diagonal principal são 1, e os demais são 0. Essa matriz funciona como o número 1 na multiplicação, pois A·I = I·A = A para qualquer matriz quadrada A de mesma ordem.

Quando trabalhamos com matrizes não quadradas, essa propriedade se aplica de maneira específica: Im·A = A (se A tem m linhas) e A·In = A (se A tem n colunas).

A matriz inversa existe apenas para algumas matrizes quadradas. Uma matriz A tem inversa (A⁻¹) quando A·A⁻¹ = A⁻¹·A = I. Para encontrar a inversa, precisamos resolver um sistema de equações que estabeleça essa condição de produto igual à identidade.

Para calcular a matriz inversa, transformamos a condição A·A⁻¹ = I em um sistema de equações. Por exemplo, se A = [2 1; 5 3] e queremos encontrar A⁻¹ = [a b; c d], precisamos resolver o sistema gerado por $2a+1c 2b+1d; 5a+3c 5b+3d$ = [1 0; 0 1].

💡 Observação importante: Nem toda matriz quadrada possui inversa! Uma matriz só tem inversa se seu determinante for diferente de zero. Matrizes que possuem inversa são chamadas de "invertíveis" ou "não-singulares".

Sistemas Lineares

Um sistema linear é um conjunto de equações do tipo a₁x₁ + a₂x₂ + ... + aₙxₙ = b, onde queremos encontrar valores para as incógnitas que satisfaçam todas as equações simultaneamente.

Geometricamente, os sistemas lineares podem ser classificados em três categorias:

• Sistema Possível e Determinado (SPD): possui uma única solução (retas se cruzam em um único ponto)
• Sistema Possível e Indeterminado (SPI): possui infinitas soluções (retas coincidentes)
• Sistema Impossível (SI): não possui solução (retas paralelas)

Todo sistema linear pode ser representado na forma matricial. Por exemplo, o sistema 5x + 4y = 1, 3x + 7y = 2 pode ser escrito como [5 4; 3 7]·[x; y] = [1; 2], ou na forma de matriz ampliada [5 4 1; 3 7 2].

Um sistema escalonado tem uma forma triangular, onde cada equação possui pelo menos uma incógnita a menos que a equação anterior. Isso facilita a resolução, pois podemos encontrar o valor da última variável e substituir nas equações anteriores.

💡 Dica de resolução: Para resolver sistemas, o escalonamento é uma técnica poderosa. Comece eliminando variáveis de baixo para cima até obter um sistema triangular, depois substitua os valores encontrados nas equações anteriores.