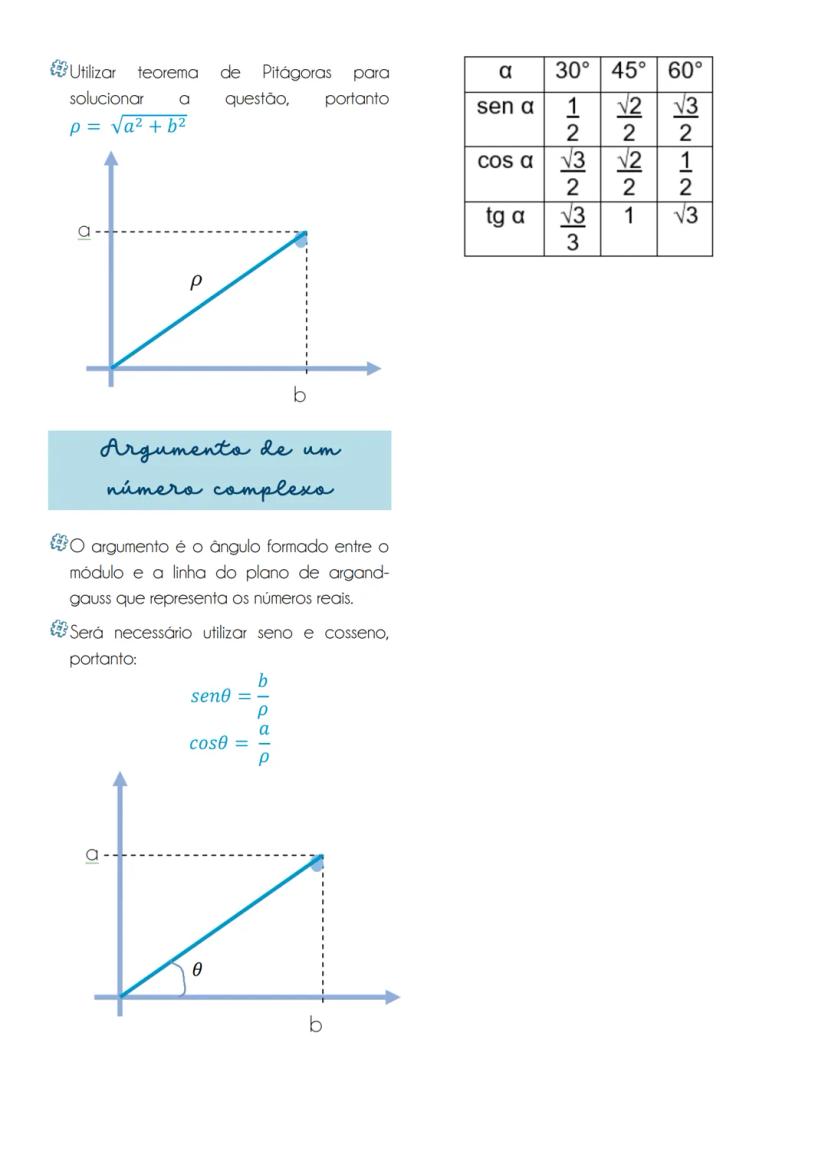
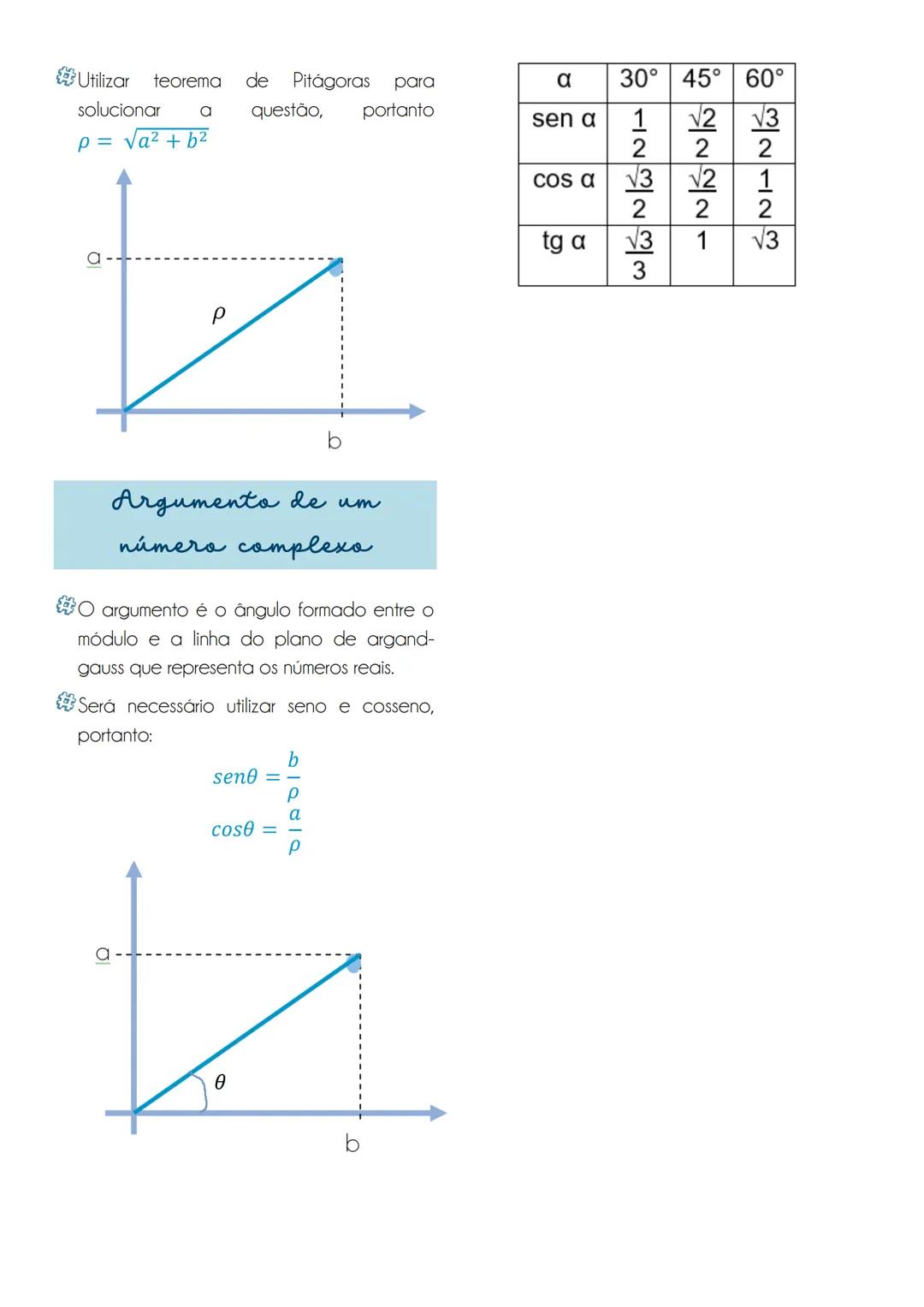
Equação Reduzida da Circunferência

A equação reduzida da circunferência é dada por $x-a$² + $y-b$² = r², onde o ponto C(a,b) representa o centro da circunferência e r é o seu raio. Esta equação vem diretamente do Teorema de Pitágoras!

Para identificar o raio e o centro em uma equação reduzida, observe que o raio é a raiz quadrada do número que está sozinho do lado direito. Por exemplo, em $x-10$² + $y-5$² = 9, temos r = 3 e o centro C(10,5).

A equação geral da circunferência é obtida quando expandimos a equação reduzida: x² + y² - 2ax - 2by + $a² + b² - r²$ = 0. Para reconhecer uma circunferência, verifique se os coeficientes de x² e y² são iguais e se não há termo xy.

Dica prática: Para identificar rapidamente o centro da circunferência na forma reduzida, basta inverter os sinais dos números que acompanham x e y!

Sobre a posição de um ponto em relação à circunferência: ele é interior quando sua distância ao centro é menor que o raio, pertence à circunferência quando a distância é igual ao raio, e é exterior quando a distância é maior que o raio.

Números Complexos

Os números complexos (representados por C) abrangem todas as outras classificações numéricas e são expressos na forma algébrica como z = x + yi, onde x é a parte real e y é a parte imaginária.

O plano de Argand-Gauss é um plano imaginário que funciona como um gráfico para representar números complexos. Neste plano, dois números complexos z₁(a,b) e z₂(c,d) são iguais apenas quando a=c e b=d.

As operações com números complexos seguem regras específicas:

• Soma e subtração: somamos/subtraímos as partes reais e as partes imaginárias separadamente
• Multiplicação: usamos a distributiva e lembramos que i² = -1
• Divisão: multiplicamos numerador e denominador pelo conjugado do denominador para eliminar o número complexo do denominador

Atenção! O conjugado de um número complexo z = a + bi é z̄ = a - bi. Esta é a chave para realizar divisões com números complexos!

O módulo de um número complexo é a distância da origem até sua representação no plano (afixo), sendo calculado por ρ = √$a² + b²$, usando o teorema de Pitágoras.

Argumento de um Número Complexo

O argumento de um número complexo é o ângulo θ formado entre o módulo e o eixo real (eixo x) no plano de Argand-Gauss. Este valor é fundamental para entender a representação geométrica do número.

Para calcular o argumento, usamos as relações trigonométricas:

• sen θ = b/ρ (parte imaginária dividida pelo módulo)
• cos θ = a/ρ (parte real dividida pelo módulo)

Estas relações vêm diretamente da trigonometria, e você pode usar a tabela de valores notáveis para ângulos comuns:

Visualize! O módulo é como o "tamanho" do número complexo, enquanto o argumento é a "direção" em que ele aponta no plano complexo.

O argumento e o módulo juntos permitem representar qualquer número complexo, o que é especialmente útil para multiplicações e divisões entre números complexos.