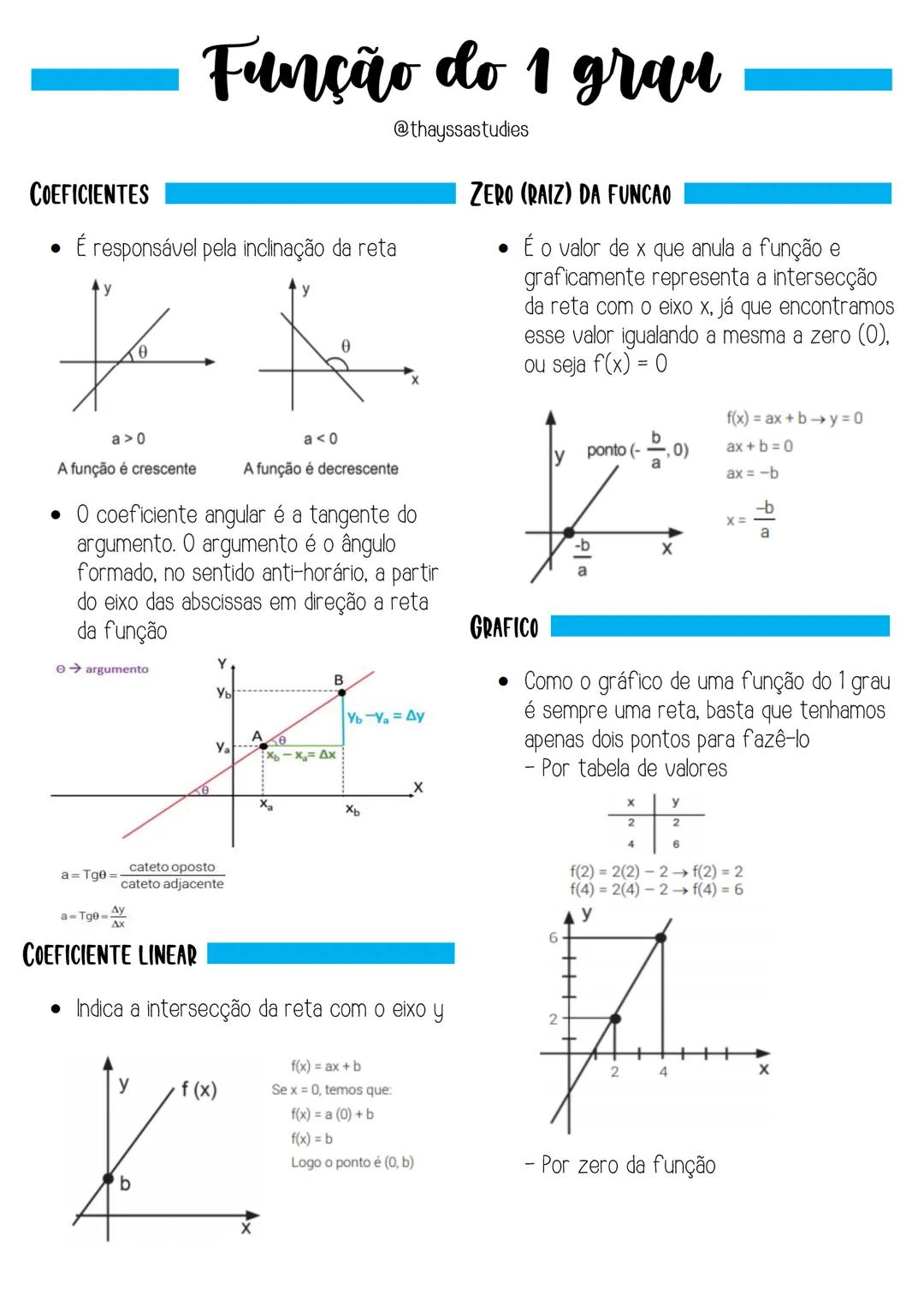
Função do 1º Grau - Coeficientes e Gráfico

Quando falamos de função de 1º grau $f(x) = ax + b$, precisamos entender os dois coeficientes que a definem. O coeficiente angular (a) determina a inclinação da reta: se a > 0, a função é crescente; se a < 0, a função é decrescente. Este coeficiente é calculado pela tangente do ângulo formado entre a reta e o eixo x: a = tg θ = Δy/Δx.

O coeficiente linear (b) indica o ponto onde a reta cruza o eixo y. Quando substituímos x = 0 na função, obtemos f(0) = b, resultando no ponto (0,b). Isso representa o valor inicial da função, antes de qualquer variação de x.

Para encontrar o zero da função (raiz), igualamos f(x) = 0. Resolvendo a equação ax + b = 0, obtemos x = -b/a. Este valor representa o ponto onde a reta cruza o eixo x, ou seja, o ponto $-b/a, 0$. Desenhar o gráfico é simples, já que uma reta é definida por apenas dois pontos. Você pode usar a raiz e o ponto (0,b), ou criar uma tabela de valores.

Dica útil: Para traçar o gráfico rapidamente, identifique primeiro o ponto (0,b) e depois calcule a raiz $-b/a$. Conecte estes dois pontos e você terá a representação gráfica completa da função!