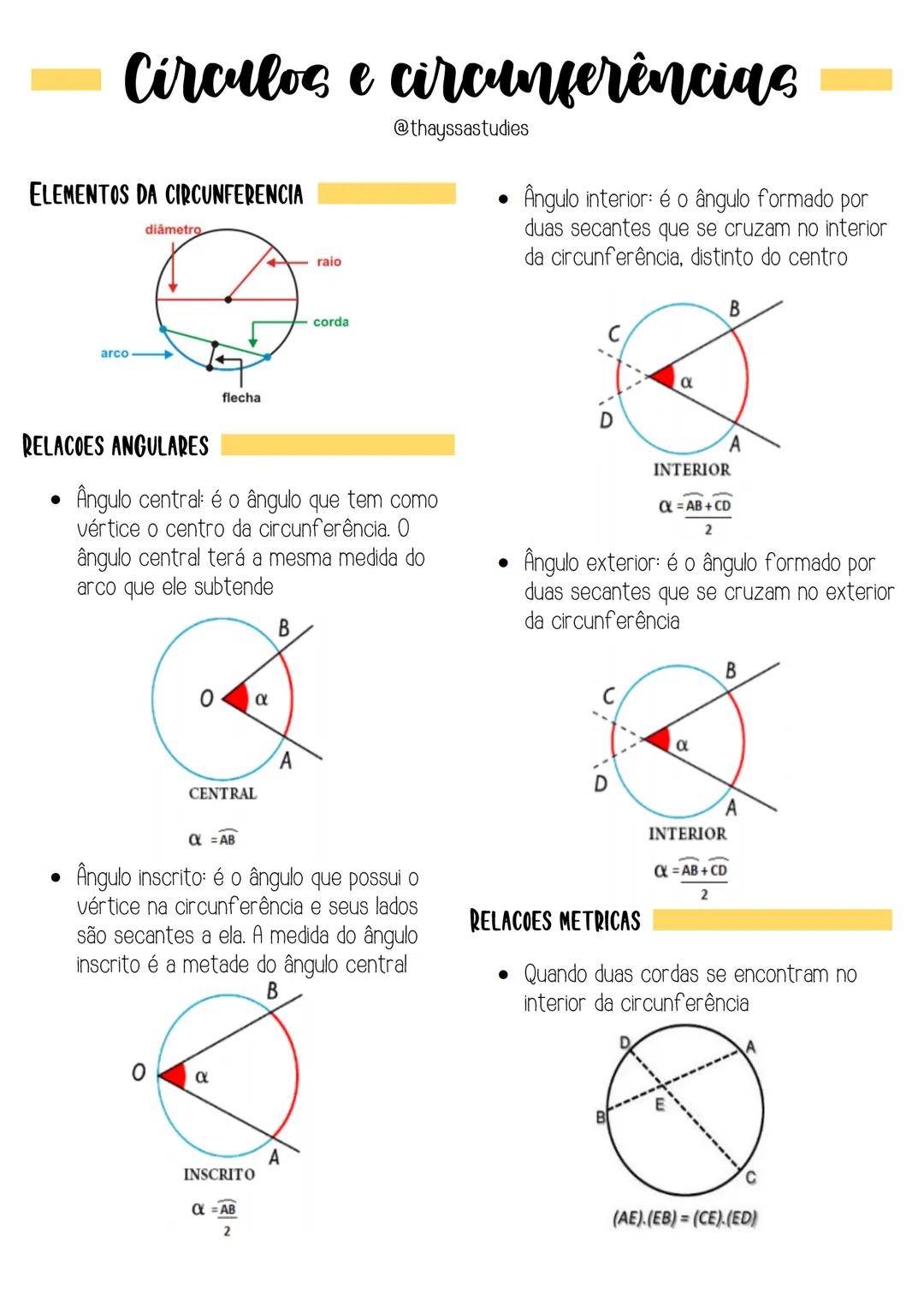
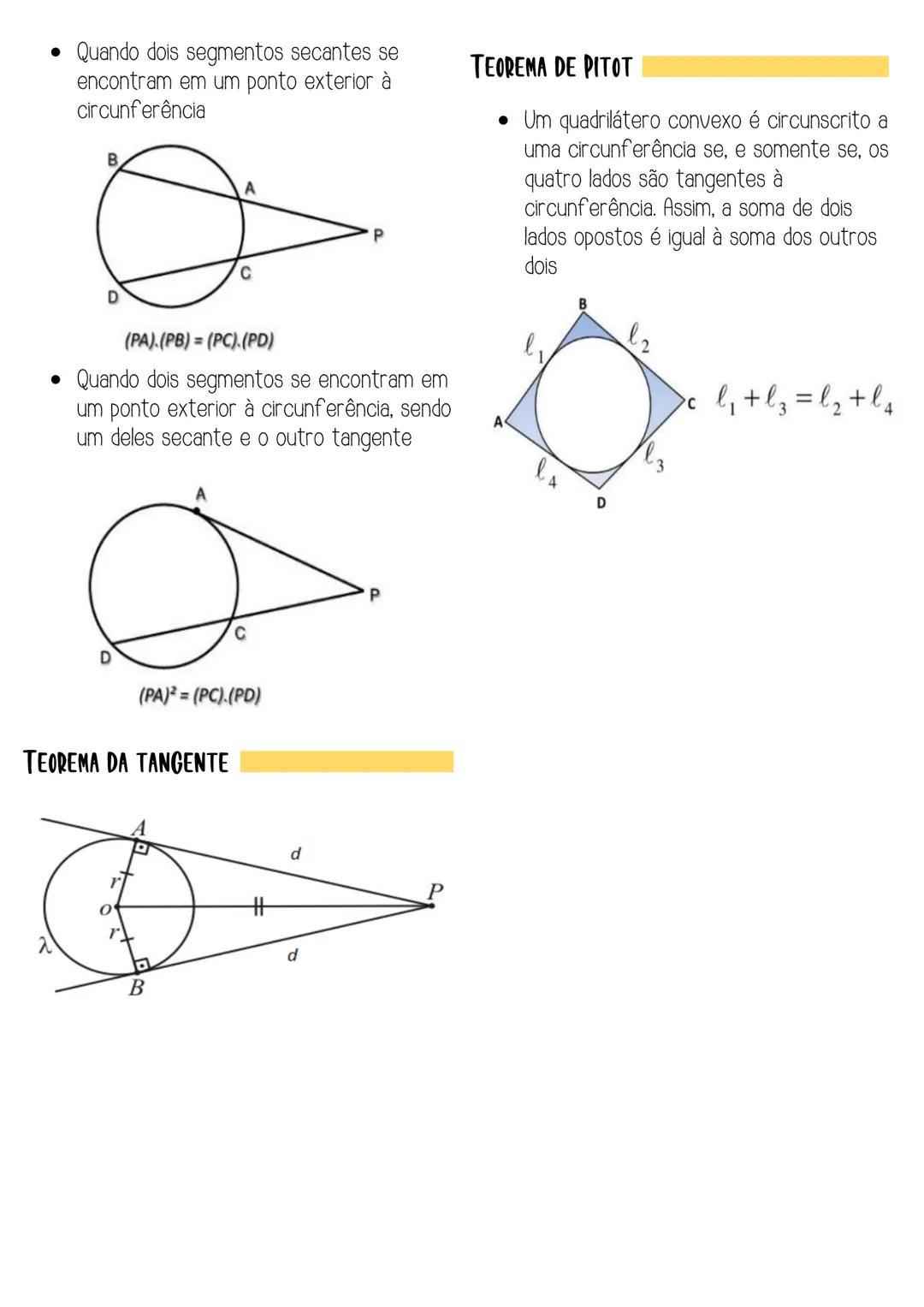
Elementos e Relações Angulares na Circunferência
Uma circunferência possui elementos básicos como raio, diâmetro, corda, arco e flecha que formam sua estrutura. Estes são fundamentais para entender qualquer problema envolvendo círculos.
As relações angulares na circunferência seguem padrões específicos. O ângulo central tem como vértice o centro da circunferência e sua medida é igual à do arco que ele determina α=AB. Já o ângulo inscrito possui vértice na própria circunferência, com seus lados secantes a ela, e sua medida é metade do ângulo central correspondente α=AB/2.
Quando analisamos o ângulo interior, formado por duas secantes que se cruzam dentro da circunferência, sua medida é igual à metade da soma dos arcos determinados α=(AB+CD)/2. De forma similar, o ângulo exterior é formado pelo cruzamento de secantes no exterior da circunferência.
💡 Dica prática: Para não confundir as relações angulares, lembre-se que o ângulo inscrito é sempre metade do central, e que ângulos interiores e exteriores dependem da soma dos arcos.