Análise Combinatória e Probabilidade

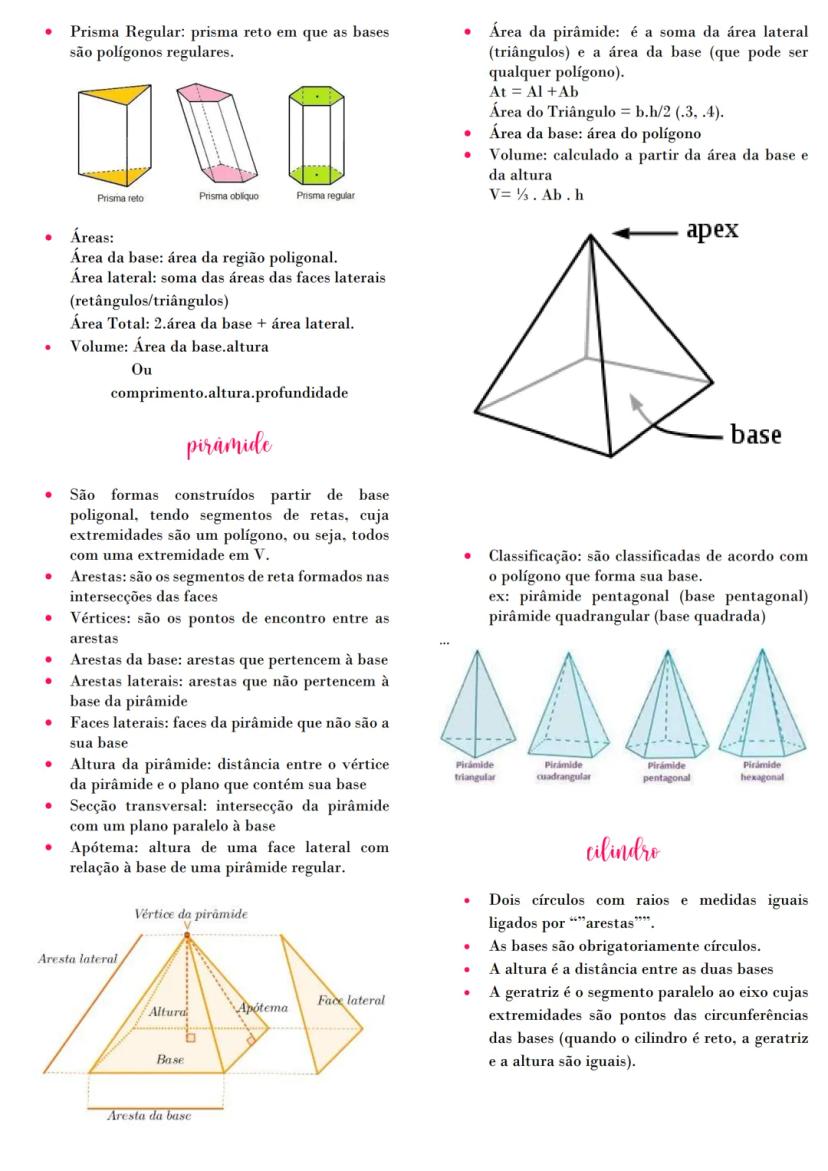
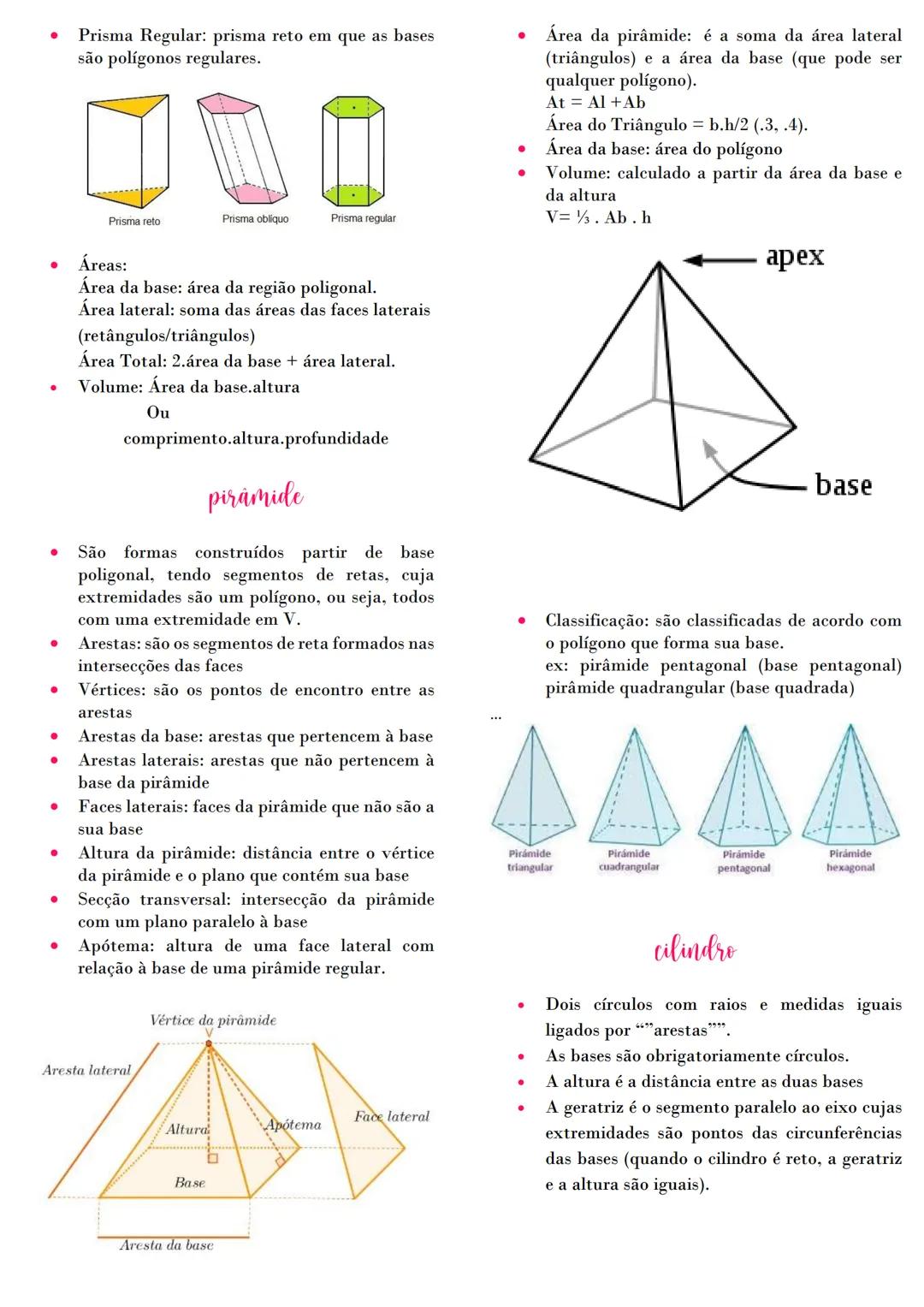
A Análise Combinatória nos ajuda a contar possibilidades de forma organizada. O fatorial (n!) é um cálculo básico muito usado, como em 7! = 7×6×5×4×3×2×1. Quando precisamos organizar elementos em ordem, usamos a permutação simples $Pn = n!$, ótima para calcular anagramas como "ROMA", que tem 4! = 24 possibilidades.

Os arranjos são agrupamentos onde a ordem importa, calculados por A(n,k) = n!/$n-k$!. Já nas combinações, a ordem não importa, usando a fórmula C(n,p) = n!/$(n-p)!×p!$. Para casos com elementos repetidos, como em "AMANDA" (com três letras "A"), usamos a fórmula 6!/3! = 120.

A Probabilidade estuda eventos aleatórios cujos resultados não podemos prever. O espaço amostral (Ω) contém todos os possíveis resultados, enquanto um evento é qualquer subconjunto desse espaço. A probabilidade é calculada pela razão entre casos favoráveis e possíveis.

Dica prática: Quando resolver problemas de probabilidade, sempre identifique primeiro o espaço amostral completo antes de calcular as chances de um evento específico!

Na união de eventos (A ∪ B), somamos as probabilidades e subtraímos a intersecção: P(A ∪ B) = P(A) + P(B) - P(A ∩ B). A probabilidade condicional calcula a chance de um evento ocorrer sabendo que outro já aconteceu.

Probabilidade e Introdução à Geometria Espacial

A probabilidade da intersecção de eventos é calculada multiplicando a probabilidade de um evento pela probabilidade condicional do outro: P(A ∩ B) = P(A|B) × P(B). Isso é muito útil em problemas como retirar duas meias não rasgadas de um cesto com 10 meias, sendo 3 rasgadas.

Quando eventos são independentes, o fato de um ocorrer não afeta a probabilidade do outro, então P(A ∩ B) = P(A) × P(B). Este conceito é fundamental para resolver problemas complexos de probabilidade no vestibular.

Na Geometria Espacial, estudamos os prismas, que são sólidos com bases formadas por polígonos iguais e paralelos. Um prisma tem suas bases conectadas por faces laterais que são paralelogramos. O nome do prisma depende do polígono da base: triangular (3 lados), quadrangular (4 lados), pentagonal (5 lados) etc.

Atenção: Em um prisma reto, as arestas laterais são perpendiculares às bases, formando faces laterais retangulares. Já no prisma oblíquo, as arestas têm inclinação diferente de 90°.

A altura do prisma é a distância entre os planos das bases. Esses conceitos são essenciais para calcular áreas e volumes, que caem frequentemente em provas.

Cilindros e Cones

Os cilindros podem ser vistos como prismas com bases circulares. Existem dois tipos principais: o cilindro reto, onde o eixo é perpendicular às bases, e o cilindro oblíquo, onde o eixo é inclinado. Você precisará calcular três medidas importantes:

• Área da base: πr²
• Área lateral: 2πrh
• Área total: 2πr$h+r$
• Volume: πr²h

Já o cone é semelhante a uma pirâmide, mas com base circular. Suas características principais incluem: uma base circular, um vértice único e geratrizes que ligam o vértice a qualquer ponto da base. A altura é a distância perpendicular do vértice à base.

Existem diferentes tipos de cones, como o cone reto (onde a altura cai no centro da base) e o cone oblíquo. Um caso especial é o cone equilátero, que tem propriedades específicas.

Visualize assim: Um cone é como um sorvete de casquinha onde a casquinha é o próprio cone e o ponto na extremidade inferior é o vértice!

Para calcular medidas do cone, use as fórmulas:

• Área da base: πr²
• Área lateral: πrg (onde g é a geratriz)
• Área total: πr$g+r$
• Volume: ⅓πr²h